Sudoku with extended rules is just what it sounds like - it’s a sudoku puzzle that has some rules added to it, making it more interesting. This allows for crazy and, at first glance, unsolvable puzzles, like this one: 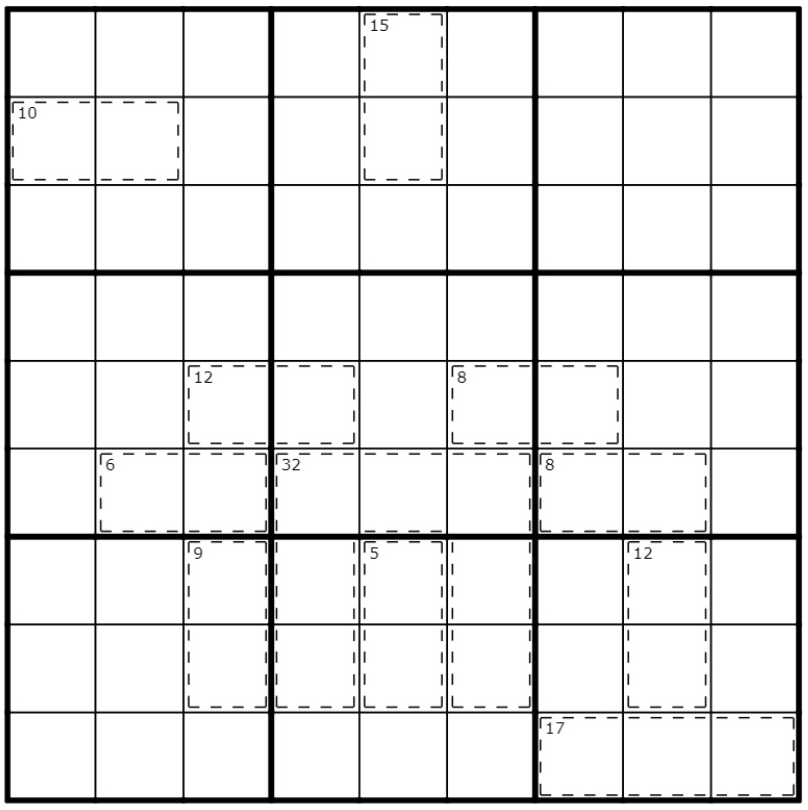
What is this post about
This post is about representing extended sudoku rules using sets. It is the first step in translating the rules to computer-understandable ones. After they are translated, I plan on using Z3 to solve these types of sudoku.
Important notes
Throughout the text, I use sets to define various rules. The names of the sets are shown in bold, and most of them have an index sub-k since more than one instance is possible in a sudoku grid. Where functions are used (e.g. sum()), I italicize the name of the function.
I also use sudokus from Logic Masters Germany, a wonderful portal for all puzzle lovers, and F-puzzles to visualize the rules.
Defining rules
Standard
Most people know standard sudoku rules. Anyways, here they are in a set notation:
First, we must define what a sudoku grid is:
Grid = {xij | 1 ≤ i,j ≤ 9, |Grid| = 81}
As expected, a sudoku grid is just a set of positions, denoted xij, with a cardinality of 81.
Next, all the positions contain digits from 1 to 9:
∀xij ∈ Grid, 1 ≤ val(xij) ≤ 9
Here, val(square) functions returns the value of a square.
There are also some restrictions on the grid. For one, you cannot repeat the same digits in a row or a column:
∀xij ∈ Grid, j ≠ k → val(xij) ≠ val(xik)
∀xij ∈ Grid, j ≠ k → val(xji) ≠ val(xki)
You also cannot repeat digits in a sudoku “box”:
∀xij,xmn ∈ Grid, (i ≠ m ∨ j ≠ n) ∧ ⌊i/3⌋ = ⌊m/3⌋ ∧ ⌊j/3⌋ = ⌊n/3⌋ → val(xij) ≠ val(xmn)
Odd, even
Let’s start with simple extended rules.
Gray circle means that the digit in it is odd. Gray square means that the digit in it is even.

The definitions are pretty easy:
val(Oddk) mod 2 = 1
val(Evenk) mod 2 = 0
Killer Cage
Killer Cages sound spooky, but in reality they are quite easy. They allow defining extra restricted regions in the grid. Here’s how they look:

And here’s how they are defined:
Cagek = {xij | 1 ≤ i,j ≤ 9}
First, digits cannot repeat within a Cage:
∀xij,xmn ∈ Cagek, (i ≠ m ∨ j ≠ n) → val(xij) ≠ val(xmn)
Also, some cages have their sums shown in the top left corner:
(sum(Cagek) = {i ∈ ℕ}) ∨ (sum(Cagek) = "?")
The sum() functions returns the sum of all the elements in a set. I use “?” to signify that the sum is not known.
Thermo
Thermometers are an interesting concept for sure. Digits along the thermometers increase starting from the bulb (the circle). That’s how they look:
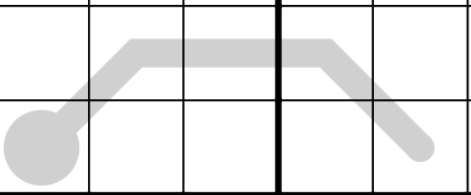
And that’s how they are defined:
Thermok = {xij | 1 ≤ i,j ≤ 9}
∀xij,xmn ∈ Thermok, xij ≺ xmn → val(xij) < val(xmn)
I cheat a little here: I define an ordering of the set, where the set is ordered from the bulb up.
Arrow
Arrows is another rule that is hard to define with just sets. The rule is simple - digits on the arrow add to the one in the bulb.
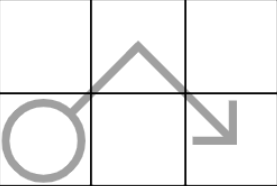
Arrowk = {xij | 1 ≤ i,j ≤ 9}
val(⊤) = sum(Arrowk - ⊤)
I cheat a little here again - I define the bulb of the arrow as the top element of the set.
Kropki dots
Kropki dots, just like XV rules (defined later) are relations between two squares of the grid. There are two types:
White Kropki, where the difference between two squares is one:
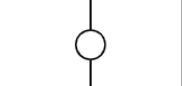
WKropkik =〈one, two〉
|WKropkik.one - WKropkik.two| = 1
And Black Kropki, where one of the squares is twice the other:
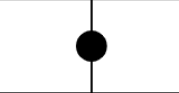
BKropkik =〈one, two〉
(BKropkik.one > BKropkik.two) ∧ (BKropkik.one = 2(BKropkik.two))) ∨ ((BKropkik.one < BKropkik.two) ∧ (2(BKropkik.one) = BKropkik.two)
I define the Kropki rules using tuples to shorten the notation.
XV Sudoku
As mentioned previously, XV rules are similar to Kropki rules. There are two different symbols:
V signifies that two squares add up to 5:
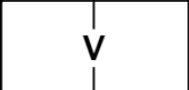
Vk =〈one, two〉
Vk.one + Vk.two = 5
X signifies that two squares add up to 10:
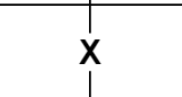
Xk =〈one, two〉
Xk.one + Xk.two = 10
Renban lines
Renban lines are simple rules that are incredibly hard to define. The rule is that the digits on the line are consequtive and are in any order (e.g. you could have 1-2-3 and 3-1-2).
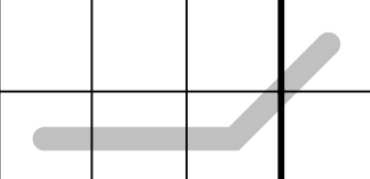
Renbank = {xij | 1 ≤ i,j ≤ 9}
∀xij ∈ Renbank, val(⊤) - |Renbank| < val(xij) ≤ val(⊤)
I have to specify here that the set is ordered by ascending value. The rule above says that all the digits on the Renban line are between top (including) and top minus the line length.
Palindrome
Palindrome rules are exacly what they sound like - squares opposite on the line are the same. The set is ordered along the line.
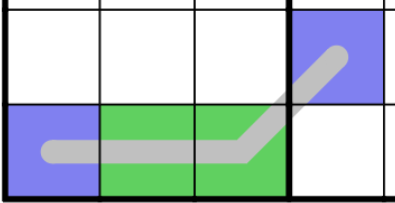
Palindromek = {xij | 1 ≤ i,j ≤ 9}
∀xij ∈ Palindromek, val(xij) = val(⊥ + (⊤ - xij))
The arithmetic on ⊤ and ⊥ calculates the “offset” of the set element.
Bishop
Bishop rules are first of the Chess Sudoku rules. The digits along a bishop move from a given digit cannot be the same.
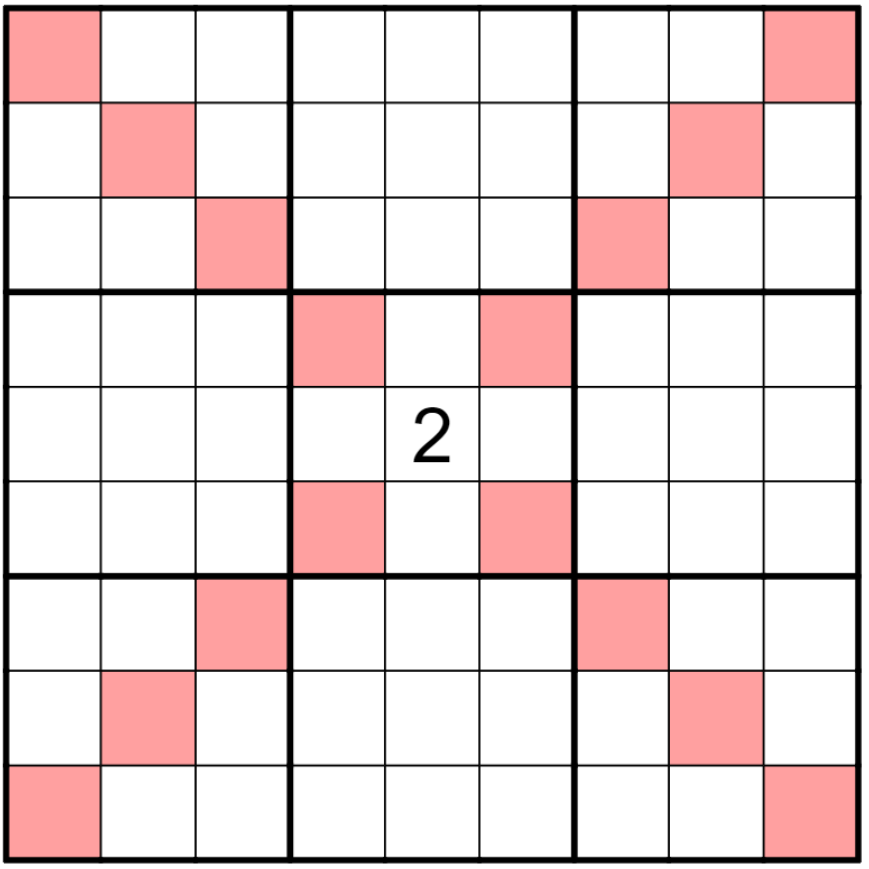
∀xij ∈ Grid, 1 ≤ n ≤ 9, xij ≠ x(i±n)(j±n)
A short note on notation: i use x ± y as a shorthand for (x + y) ∧ (x - y). Also, it is assumed that if the offset is out of the grid, the case is not considered.
King
King rules are analogous to other chess sudoku rules. The digits along a king move from a given digits cannot be the same.
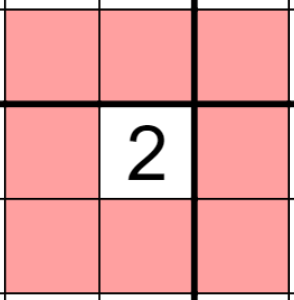
∀xij ∈ Grid, xij ≠ x(i±1)(j±1) ∧ xij ≠ x(i±1)j ∧ xij ≠ xi(j±1)
Queen
Just as in chess, queen rules are like an extention of king rules with bigger offsets.
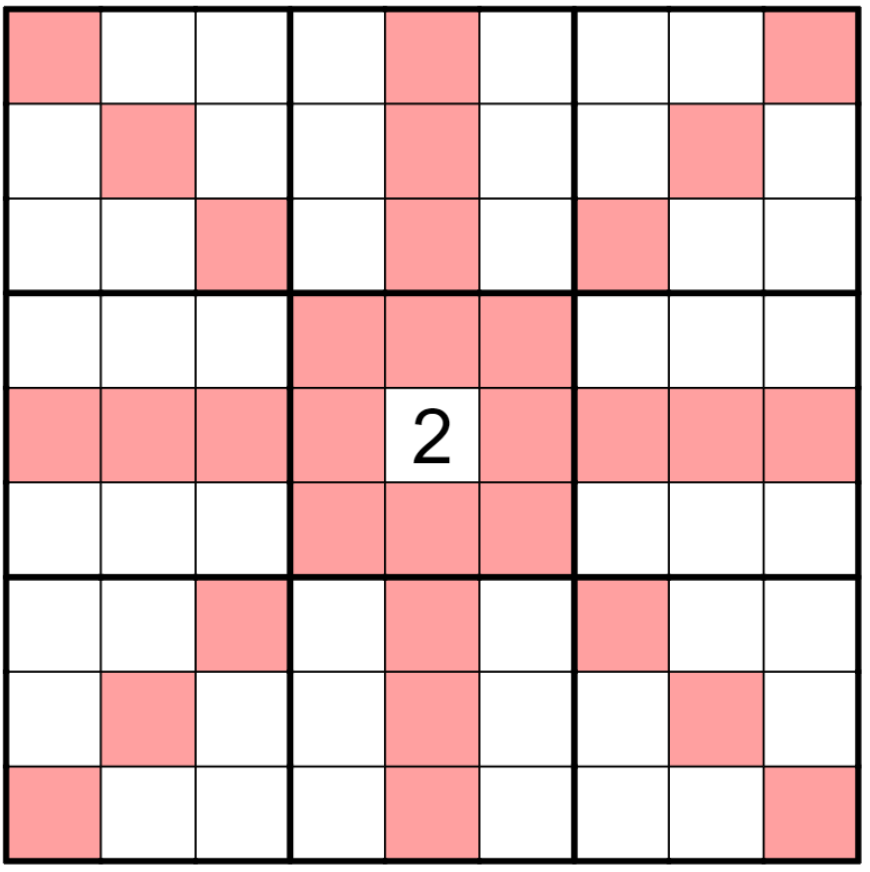
<code”>∀xij ∈ Grid, 1 ≤ n ≤ 9, xij ≠ x(i±n)(j±n) ∧ xij ≠ x(i±n)j ∧ xij ≠ xi(j±n)</code>
Knight
Again, knight sudoku rules are equivalent to their chess counterparts. Digits knight move away from each other cannot be the same.
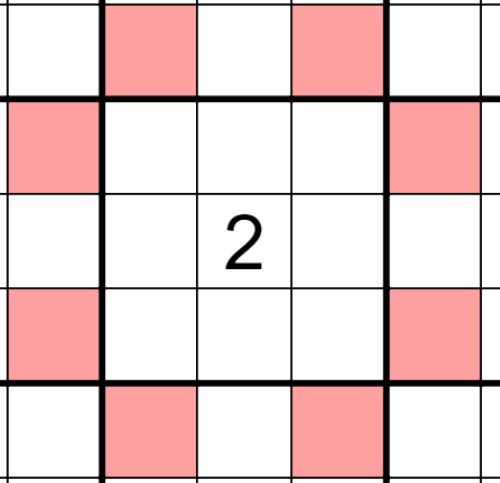
∀xij ∈ Grid, xij ≠ x(i±1)(j±2) ∧ xij ≠ x(i±2)(j±1)
Sandwich
The sandwich rule is a fun one. It says that in an indicated row/column, the numbers between 1 and 9 must sum to the clue. For example, in the case below, you can deduce that 8 has to go between 1 and 9:

SandRowi ∈ ℕ
val(xij) = 1 ∧ val(xik) = 9, SandRowi = sum({xiq | min(j, k) < q < max(j, k)})
SandColi ∈ ℕ
val(xji) = 1 ∧ val(xki) = 9, SandColi = sum({xqi | min(j, k) < q < max(j, k)})
Killer Sum
Killer sums indicate that, on the marked diagonal, the squares sum up to the given clue.
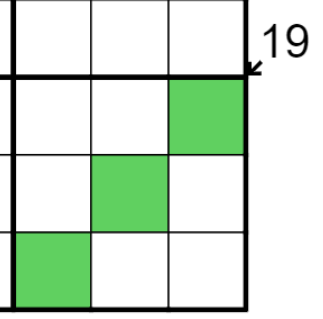
It is a bit hard to define in terms of sets, so here is my definition.
First, a Killer Sum is a 3-tuple that contains the sum itself, the starting square and the end square.
Killerk =〈sum, xij, xmn〉
Next, there are four possible cases:
(i < m ∧ j < n → sum({x(i+l)(j+l) | 0 ≤ l ≤ |i - m|}) = Killerk.sum) ∨
(i < m ∧ j > n → sum({x(i+l)(j-l) | 0 ≤ l ≤ |i - m|}) = Killerk.sum) ∨
(i > m ∧ j < n → sum({x(i-l)(j+l) | 0 ≤ l ≤ |i - m|}) = Killerk.sum) ∨
(i > m ∧ j > n → sum({x(i-l)(j-l) | 0 ≤ l ≤ |i - m|}) = Killerk.sum)
Foreword
As you can see, extensions to sudoku rules are not hard to implement. There are quite some ways to go from sets to Z3 rules, however. I plan on doing a full Python implementation of the above rules, which I will link to later on.
I would also like to thank Mark and Simon from Cracking the Cryptic YouTube channel for introducing me to the world of extended sudoku.